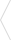مرور سریع و کامل مشتق | 12 صفحه رنگی | فقط 5000 تومان
مرور سریع و کامل مشتق | 12 صفحه رنگی | فقط 5000 تومان
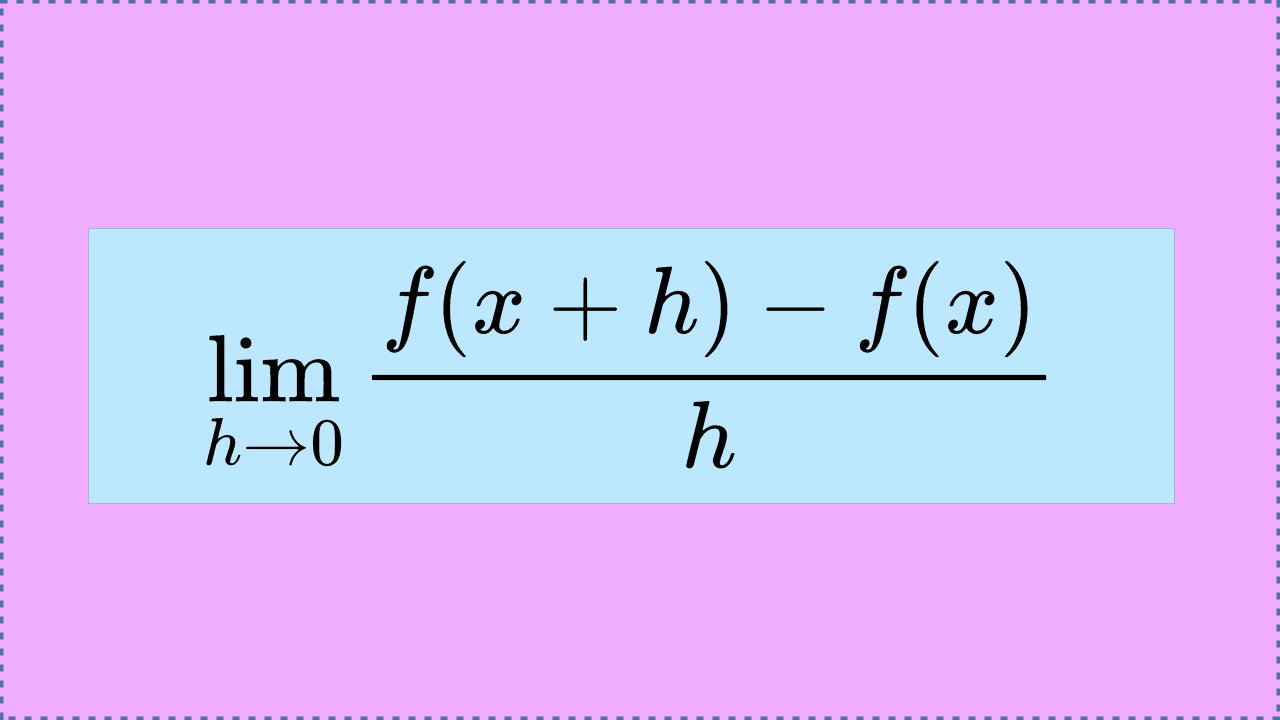
مرور سریع و کامل مشتق | 12 صفحه رنگی | فقط 5000 تومان
فرمول های مشتق مهم + سوال با جواب و دانلود PDF
مشتق، یکی از مفاهیم مهم و پرکاربرد در دنیای ریاضیات است. این مفهوم، در سطوح متوسطه و به همراه مفاهیم دیگری نظیر حد و پیوستگی آموزش داده میشود. مشتق توابع مختلف، فرمولهای مخصوص به خود را دارند. درک مبانی به دست آوردن این فرمولها و به خاطر سپردن مهمترین آنها، شما را به حل بسیاری از مسائل مرتبط در این حوزه کمک میکند.
در این مقاله، به معرفی مهمترین فرمول های مشتق به همراه حل چندین مثال و تمرین میپردازیم. علاوه بر این، فایل PDF پرکاربرترین فرمولها و قوانین مشتقگیری را ارائه میکنیم. با مطالعه این فایل میتوانید فرمول های مهم مشتق گیری را به سرعت مرور کنید.
مشتق چیست ؟
«مشتق» (Derivative)، نرخ تغییرات یک تابع نسبت به یک متغیر است. اگر بخواهیم مشتق را به زبان سادهتر تعریف کنیم، میتوانیم بگوییم که این مفهوم ریاضی، شیب نمودار در یک نقطه را نمایش میدهد. برای درک بهتر مفهوم مشتق، نمودار زیر را در نظر بگیرید.
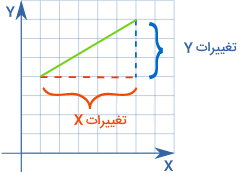

شیب نمودار (خط سبز) در تصویر بالا، از تقسیم تغییرات Y بر تغییرات X به دست میآید:
تغییرات X ÷ تغییرات Y = شیب
شیب میانگین بین دو نقطه از یک نمودار نیز با استفاده از رابطه بالا به دست میآید. به عنوان مثال، نمودار زیر را به همراه اعداد نمایش داده شده در نظر بگیرید.
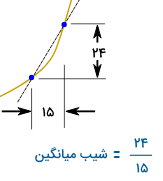

دو نقطه مشخص شده بر روی نمودار، در راستای Y و X با یکدیگر اختلاف دارند. با تقسیم اختلاف در راستای Y بر اختلاف در راستای X، شیب میانگین بین این دو نقطه به دست میآید. در صورت نزدیکی خیلی زیاد دو نقطه به یکدیگر، اختلاف آنها در هر دو راستا، تقریبا برابر با صفر میشد.
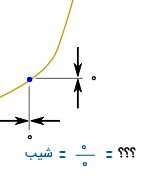

در مثال بالا، چیزی برای اندازهگیری وجود ندارد. با این حال، اگر دو نقطه را از نمای بسیار نزدیک نگاه کنیم، اختلاف جزئی بین آنها نمایان میشود. در ریاضیات، این اختلافهای جزئی را با Δ نمایش میدهند.
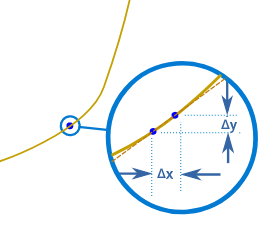

اکنون میتوانیم شیب میانگین بین دو نقطه را به دست بیاوریم. این شیب، عبارت است از:
�=Δ�Δ�
m، علامت مورد استفاده برای نشان دادن شیب در روابط ریاضی است. اکنون میتوانیم از این رابطه برای گرفتن مشتق توابع استفاده کنیم. تابع زیر را در نظر بگیرید:
�=�(�)
برای به دست آوردن مشتق تابع بالا، دو نقطه بسیار نزدیک بر روی نمودار آن را در مشخص میکنیم.
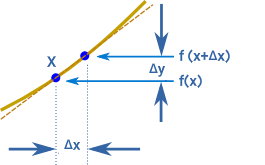

با توجه نمودار، اختلاف دو نقطه در راستای X از x تا x+Δx و اختلاف دو نقطه در راستای Y از f(x) تا f(x+Δx) است. برای به دست آوردن مشتق تابع، مراحل زیر را انجام میدهیم:
- قرار دادن تابع در فرمول Δ�Δ�=�(�+Δ�)−�(�)Δ�
- سادهسازی و باز کردن عبارتها تا حد ممکن
- برابر قرار دادن Δx با صفر

درباره این محصول نظر دهید !
- توضیحات محصول را به خوبی بخوانید و در صورت نیاز به راهنمایی از بخش کاربری و سیستم تیکت استفاده نمایید .
- پشتیبانی محصولات سیستم تیکت و تماس از طریق واتس آپ می باشد .
- برای دریافت آخرین نسخه محصولات و دسترسی همیشگی به محصولات خریداری شده حتما در سایت عضو شوید .
- پرداخت از طریق درگاه بانکی انجام میشود در غیر این صورت با ما تماس بگیرید