دانلود کتاب معادلات دیفرانسیل بویس | 20 میشم

 

 

فایل مورد نظردر قالب pdf  با حجم 9.5 مگابایت می باشد. دوستان گرامی و دانشجویان ارجمند و عزیز در صورت تمایل می توانید این فایل بسیار با ارزش را به صورت مستقیم از سایت بیست میشم تهیه بفرمائید.

 

کتاب معادلات دیفرانسیل بویس به زبان فارسی

شامل 425 صفحه PDF

 

 

دانلود کتاب معادلات دیفرانسیل بویس | 20 میشم

 

 

 

 

 

 

حل شدن یک معادله دیفرانسیل به چه معناست؟

دانلود کتاب معادلات دیفرانسیل بویس | 20 میشم بیان دارد زمانی یک معادله دیفرانسیل حل شده است که تابع y بر حسب متغیر‌های وابسته‎‌اش پیدا شده باشد.

به طور دقیق‌تر، یعنی اینکه بدانیم مثلا y که تابعی از متغیر x در نظر گرفته‌شده، طبق کدام رابطه توصیف می‌شود. روش‌های متفاوتی به منظور حل یک معادله دیفرانسیل وجود دارند، اما در ابتدا بایستی بدانیم که چرا معادلات دیفرانسیل مهم هستند.

 

 

دانلود کتاب معادلات دیفرانسیل بویس | 20 میشم

دانلود ترجمه کتاب معادلات دیفرانسیل بویس

چرا معادلات دیفرانسیل مفید هستند؟

طبق دانلود کتاب معادلات دیفرانسیل بویس | 20 میشم در دنیایی زندگی می‌کنیم که پدیده‌ها دائماً در حال تغییر هستند. این در حالی است که می‌توان اکثر این دگرگونی‌ها را با استفاده از معادلات دیفرانسیل توصیف کرد.

به عنوان مثال، آلبرت انیشتین به منظور توصیف نیروی گرانشی از معادلات دیفرانسیل استفاده کرد؛ او به کمک این معادلات هم این نیرو را توضیح داد و هم ثابت کرد که امکان سفر به آینده امکان‌پذیر است! در ادامه، دو مثال کاربردی از این معادلات ارائه می‌دهیم.

مثال ۱: رابطه بین جمعیت خرگوش‌ها و معادله دیفرانسیل

هرچه خرگوش بیشتری وجود داشته باشد، بچه خرگوش بیشتری نیز وجود خواهد داشت.

این بچه‌ خرگوش‌ها نیز بزرگ خواهند شد و تولید مثل خواهند کرد. بنابراین با گذشت زمان تعداد خرگوش‌ها بیشتر و بیشتر خواهند شد.

خب اجازه دهید ببینیم این روند زیاد شدن به چه شکل و با چه سرعتی اتفاق می‌افتد. به این منظور در ابتدا فرضیات زیر را در نظر می‌گیریم.

• N: تعداد خرگوش‌ها در زمان t
• r: نرخ تولد (منظور از نرخ تولد، تعداد خرگوش‌هایی است که یک خرگوش و در یک بازه‌ زمانی معین تولید می‌کند.)
• dN/dt: سرعت زیاد شدن تعداد کل خرگوش‌ها

 

دانلود قوی ترین کتاب آشنایی با نظریه گراف

 

 

درس معادلات دیفرانسیل مقدماتی وسیله ای است بسیار عالی برای اینکه دانشجو بتواند ارتباط بین ریاضیات محض و علوم فیزیکی یا مهندسی را درک کند. پیش از آنکه مهندس یا دانش پژوهی بتواند با اعتماد به کاربرد معادلات دیفرانسیل بپردازد، باید به روش های حل آنها تسلط پیدا کند و حداقل از نظر زیربنایی این مبحث اطلاع مجملی داشته باشد.

 

این مجموعه ویژه شامل ۲ ویرایش کتاب معادلات دیفرانسیل مقدماتی نوشته ی ویلیام ای بویس به همراه نسخه فارسی کتاب است که به رایگان از طریق سایت پروژه ها می توانید دانلود نمائید.

 

 

 

حال این اعداد را در قالب یک مثال واقعی فرض کنید:

• در حال حاضر تعداد کل خرگوش‌ها برابر با N=1000 است.
• هر خرگوش در یک هفته r=0.01 بچه تولید می‌کند.

با دو فرض در نظر گرفته شده در بالا، می‌توان نتیجه گرفت که کل خرگوش‌ها در هر هفته، تعداد dN/dt=1000×0.01=10 بچه جدید به وجود می‌آورند. توجه کنید که این اعداد فقط با یک مقطع زمانی معین ارتباط دارند و به این معنی نیستند که خرگوش‌ها دائماً در حال افزایش هستند.

بنابراین، بهتر است بگوییم که نرخ زیاد شدن تعداد خرگوش‌ها  در هر لحظه برابر است با: dN/dt=rN.اگر خوب دقت کنید، این رابطه یک معادله دیفرانسل محسوب می‌شود چرا که در آن (N(t به صورت تابعی از مشتقاتش بیان شده است.

این جا است که به قدرت ریاضیات پی می‌بریم. این معادله می‌گوید: «نرخ رشد جمعیت خرگوش‌ها بر واحد زمان برابر با حاصل ضرب نرخ رشد در تعداد آن‌ها است.»

معادلات دیفرانسیل به ما می‌گویند که چگونه جمعیت زیاد می‌شود، حرکت گرما به چه شکل است، فنر طبق کدام الگو نوسان می‌کند و به همین ترتیب تجزیه شدن مواد رادیواکتیو و بسیاری دیگر از پدیده‌ها را توصیف می‌کنند.

لازم به ذکر است که این معادلات، طبیعی‌ترین راه به منظور نشان دادن مکانیزم کارکرد کائنات هستند. در ادامه به بررسی مثالی کاربردی می‌پردازیم که ممکن است روزی به کمک‌تان بیاید.

مثال ۲: بهره مرکب

اندوخته پولی، منجر به ایجاد بهره خواهد شد؛ بهره این اندوخته را می‌توان سالانه، ماهانه و به شیوه‌های دیگر محاسبه کرد. نهایتا بهره محاسبه شده به مقدار اولیه اضافه خواهد شد. این مفهوم، بهره مرکب نامیده می‌شود.

زمانی که بهره به صورت دائمی وجود داشته باشد، میزان اندوخته انباشه شده در زمان نیز، پیوسته افزایش می‌یابد.

این در حالی است که هرچه اندوخته بیشتر باشد، بهره به دست آمده نیز بیشتر خواهد بود. به منظور درک بهتر به مثال ارائه شده در ادامه توجه فرمایید. در این مثال از نماد‌های زیر استفاده می‌کنیم:

• t: زمان
• r: نرخ بهره
• V: مقدار سرمایه اندوخته شده

با توجه به فرض صورت گرفته، می‌توان میزان سرمایه ذخیره شده در واحد زمان را با استفاده از رابطه زیر توصیف کرد:

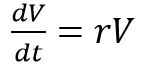
نکته جالب اینکه رابطه مورد اشاره بسیار شبیه به تفسیر معادلات دیفرانسیل در مورد زیاد شدن خرگوش‌ها است و فقط نماد‌ها هستند که تغییر کرده‌اند. بنابراین ریاضیات به ما نشان می‌دهد که چگونه دو پدیده می‌توانند مشابه یکدیگر رفتار کنند.

 

دانلود کتاب معادلات دیفرانسیل بویس | 20 میشم

 

 

 

حرکت نوسانی ساده

باتوجه به دانلود کتاب معادلات دیفرانسیل بویس | 20 میشم در فیزیک، مبحثی به نام «حرکت دوره‌ای» (Periodic Motion) وجود دارد. ساده‌ترین نوع این حرکت، «حرکت نوسانی ساده» (Simple Harmonic Motion) است. به منظور تحلیل و بررسی سیستم جرم و فنر، آن را به صورت نوسانی ساده در نظر می‌گیرند.

در چنین سیستمی نیروی ذخیره شده در فنر با افزایش طول آن زیاد می‌شود.

در ابتدا فنری را در نظر بگیرید که جرمی به آن متصل شده‌ است. با توجه به این فرض، نوسان جرم طی مراحل زیر اتفاق خواهد افتاد:

• این جرم به دلیل نیروی گرانشی به سمت پایین کشیده می‌شود.
• به دلیل زیاد شدن طول فنر، نیروی کششی در آن افزایش می‌یابد.
• به تدریج سرعت جرم، کم خواهد شد.
• نیروی کششی موجود در فنر، جرم را به سمت بالا می‌کشد.
• دوباره جرم به سمت پایین حرکت خواهد کرد و مرتبا این مراحل تکرار خواهند شد.

 

 

دانلود کتاب معادلات دیفرانسیل بویس | 20 میشم

دانلود ترجمه کتاب معادلات دیفرانسیل بویس

 

دسته‌بندی معادلات دیفرانسیل

چگونه یک معادله دیفرانسیل حل می‌شود؟ بدیهی است که همیشه پاسخ به این سوال آسان نخواهد بود. از سال‌های دور تاکنون افراد زیادی به دنبال راه‌حل‌های جدیدی به منظور حل این معادلات بوده‌اند. بنابراین به منظور تسلط بر موضوع بایستی با نوع یک معادله آشنا باشیم.

تصور کنید که می‌خواهید به مسافرت بروید. احتمالا با روش‌های مختلفی می‌توانید این کار را انجام دهید. مثلا سفر با هواپیما، خودرو شخصی و یا حتی ممکن است با پای خود قصد سفر کنید.

البته اگر هدف شما سفر به کهکشان دیگری باشد احتمالا بایستی چند صد سال منتظر بمانید تا ابزار مناسب این سفر اختراع شود!

حل کردن معادلات دیفرانسیل نیز همانند سفر رفتن است و احتمال دارد با چند روش بتوانید یک معادله دیفرانسیل را حل کنید. بنابراین قصد داریم در این قسمت انواع مختلف معادلات دیفرانسیل را معرفی کنیم.

ساده یا پاره‌ای

قبل از حل معادلات دیفرانسیل مهم‌ترین کار این است که بدانیم این معادله ساده یا با مشتقات جزئی است.

• معادلات دیفرانسیل ساده (ODE)، به معادلاتی گفته می‌شود که در آن یک متغیر مستقل وجود داشته باشد.
• معادلات دیفرانسیل با مشتقات پاره‌ای (PDE)، معادلاتی هستند که در آن‌ها دو یا چند متغیر مستقل وجود داشته باشد.

مرتبه و درجه یک معادله دیفرانسیل

در ادامه به دو مشخصه مهم یک معادله دیفرانسیل، یعنی «مرتبه» (Order) و «درجه» (Degree) خواهیم پرداخت.

مرتبه

مرتبه، بالاترین مشتق گرفته‌شده از تابع وابسته، در یک معادله است. به عنوان مثال معادله زیر از مرتبه اول است چراکه بزرگ‌ترین مشتق موجود در آن، مشتق اول تابع y نسبت به متغیر dy/dx) x) است.

خطی بودن یک معادله

به معادله دیفرانسیلی خطی گفته می‌شود که تمام توابع و مشتقات موجود در آن خطی باشند. عباراتی که در زیر آمده‌اند، معادله را غیر خطی می‌کنند.

 

IRT 5,000 – خرید نهایی کردن خرید مورد به سبد خرید اضافه شد