مطلب پیشنهادی عالی برای شما :
دانلود Pdf کتاب معادلات دیفرانسیل | حسین فرامرزی
دانلود و خرید PDF کتاب ریاضی عمومی ۱ | حسین فرامرزی
معادله دیفرانسیل | کامل ترین مقاله
در ریاضیات، معادله دیفرانسیل نوعی معادلهٔ ریاضی است که دارای یک (یا چند) تابع مجهول از یک یا چند متغیّر مستقل و مشتقهای آن توابع (با مرتبههای مختلف) است.
این معادلات در مدلسازی ریاضیاتی بسیاری از پدیدههای طبیعی کاربرد دارند. بسیاری از قوانین عمومی طبیعت (در فیزیک، شیمی، زیستشناسی و ستارهشناسی) طبیعیترین بیان ریاضی خود را در زبان معادلات دیفرانسیل مییابند. از جمله کاربردهای آن میتوان به مدارهای الکتریکی، سرعت حدّی، غلظت مواد شیمیایی و رشد جمعیّت اشاره کرد. معادلات دیفرانسیل همچنین در هندسه و نیز در مهندسی و بسیاری از حوزههای دیگر کاربردهای فراوانی دارند.
هر زمان که نرخ تغییرات یک (یا چند) تابع رابطهای با خود یا متغیّرهای خود داشته باشد، آن پدیده با معادلهٔ دیفرانسیل مدلسازی میشود.
به عنوان مثال در مکانیک، حرکت جسم به وسیله سرعت و مکان آن در زمانهای مختلف توصیف میشود و معادلات نیوتن به ما رابطهٔ بین مکان و سرعت و شتاب و نیروهای گوناگون وارده بر جسم را میدهند. در چنین شرایطی میتوانیم حرکت جسم را در قالب یک معادلهٔ دیفرانسیلی که در آن مکان ناشناختهٔ جسم تابعی از زمان است بیان کنیم.
پیدا کردن جواب


تابع انتگرال سینک به صورت {\displaystyle \operatorname {Si} (x)=\int {\sin(x) \over x}\operatorname {d} \!x} تعریف میشود.
برای بسیاری از معادلات دیفرانسیل، ممکن است جوابی وجود نداشته باشد یا جوابشان یکتا نباشد. در صورتی که جواب یکتا وجود داشته باشد نیز، در اکثر مواقع اثبات میشود که جواب به صورت یک تابع مقدّماتی قابل بیان نیست.
به عنوان مثال، جواب معادلهٔ دیفرانسیل {\displaystyle y’={\sin(x) \over x}} را تابع انتگرال سینوس مینامیم {\displaystyle y=\operatorname {Si} (x)}. با وجود این که این تابع یک تابع مقدّماتی نیست، همهٔ خصوصیات این تابع با کامپیوتر قابل محاسبه اند (که در این مورد با توابع مثلّثاتی و نمایی تفاوتی ندارد).
در حقیقت، تابع نمایی نیز به این صورت تعریف میشود: تابعی که در معادلهٔ دیفرانسیل {\displaystyle y’=y} صدق کند را {\displaystyle \exp(x)} مینامیم ({\displaystyle e^{x}=\exp(x)=y}). در نتیجه ریاضیدانان جواب معادلات دیفرانسیل پرکاربرد را نامگذاری میکنند. به عنوان مثالی دیگر میتوان به توابع بسل اشاره کرد.
بنابرین، جواب اکثر معادلات دیفرانسیل خود یک تابع جدید است که با روشهای عددی (تقریبی) و کامپیوتری (مانند روشهای رونگه-کوتا) حل میشوند (از روشهای دیگر عددی میتوان به روش اویلر، روش هون، روش تیلور، آدامز-بشفورث-مولتون، روش میلن سیمپسون، روش هامینگ، روش رانگ-کوتا فلبرگ مرتبه ۵، روش رحمانزاده کای وایت، روشهای طیفی و شبه طیفی، روشهای شبکهای همانند اجزای محدود و تفاضل محدود و روشهای بدون شبکه اشاره کرد).
در صورتی که جواب یک معادله وجود داشته باشد و یکتا باشد و به صورت یک تابع مقدّماتی قابل بیان باشد، برای پیدا کردن آن از روشهای حل تحلیلی استفاده میشود (تنها برای سادهترین معادلات دیفرانسیل جواب صریح وجود دارد).
در این حالت نیز یک راه حل کلّی برای حل تمام معادلات دیفرانسیل (قابل حل تحلیلی) وجود ندارد. دلیل این موضوع میتواند این باشد که هنوز چنین راه حلّی کشف نشده باشد یا این که چنین راه حل کلّی وجود نداشته باشد. به همین دلیل این معادلات به چند دسته تقسیم میشوند که برای هر کدام راه حلّی کشف شدهاست.
مطلب پیشنهادی عالی برای شما :
دانلود Pdf کتاب معادلات دیفرانسیل | حسین فرامرزی
دانلود و خرید PDF کتاب ریاضی عمومی ۱ | حسین فرامرزی
بعضی از معادلات دیفرانسیل در هیچکدام از این دستهها نیز قرار نمیگیرند و راه حلّی (تحلیلی) برای آنها وجود ندارد. در این میان روشهای نیمهتحلیلی نیز وجود دارد که از آنها میتوان به روش تجزیه آدومیان، آنالیز هموتوپی، تبدیل دیفرانسیل اشاره کرد.
در نتیجه، برای حل یک معادلهٔ دیفرانسیل ابتدا باید بررسی کنیم که آیا جواب یکتا برای آن وجود دارد یا خیر و سپس این که در چه شاخهای قرار دارد. اگر برای شاخهٔ مورد نظر حل تحلیلی وجود داشت، از آن روش استفاده میکنیم و در غیر این صورت از روشهای عددی استفاده میکنیم. مسلّماً اگر جواب عددی برایمان کافی باشد، میتوانیم از همان ابتدا از روش عددی استفاده کنیم.
مسائل مقدار اولیه
در حل مسائل کلّی به ثابت انتگرال برمیخوریم. به عنوان مثال:
{\displaystyle y’=1\Longrightarrow y=\int 1\operatorname {d} \!x+c=x+c}
به این معنی که مقدار پادمشتق میتواند هر تابع {\displaystyle x+c} (به ازای هر {\displaystyle c}) باشد. به عبارتی دیگر تابع {\displaystyle y} ممکن است {\displaystyle y=x+1} یا {\displaystyle y=x+2} یا موارد مشابه باشد.
در صورتی که مقدار اوّلیّهٔ {\displaystyle y} را بدانیم، میتوان آن را به صورت دقیق پیدا کرد. در مثال قبلی، اگر بدانیم {\displaystyle y(1)=2} از این موضوع نتیجه میگیریم:
{\displaystyle y(x)=x+c\Longrightarrow y(1)=1+c=2\Longrightarrow c=1\Longrightarrow y(x)=x+1}
به عنوان مثال، اگر بدانیم سرعت یک جسم ({\displaystyle y’}) برابر ۱ است و همچنین در ثانیهٔ ۱ در مکان ۲ قرار داشته ({\displaystyle y(1)=2})، از روش مذکور برای پیدا کردن معادلهٔ مکان-زمان استفاده میکنیم.
شاخهبندی
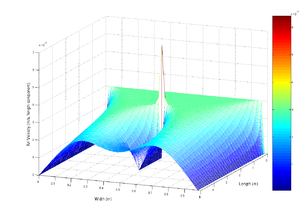

مجسمسازی جریان هوا به داخل لوله که با معادلات ناویه-استوکس، مدلسازی شدهاست، مجموعهای از معادلات دیفرانسیل با مشتقات جزئی
معادلات دیفرانسیل را بهطور کلی به دو دسته میتوان تقسیم کرد:
- معادلات دیفرانسیل معمولی (به انگلیسی: ordinary differential equation): در این نوع معادلات تابع پاسخ دارای تنها یک متغیّر مستقل است. یک معادله شامل یک متغیّر مستقل {\displaystyle x}، تابع {\displaystyle y(x)} و مشتقات آن را یک معادله دیفرانسیل عادی یا معمولی (به انگلیسی: ODE) مینامند.
- معادلات دیفرانسیل با مشتقات جزئی (به انگلیسی: partial differential equation): در این نوع معادلات تابع پاسخ دارای چندین متغیّر مستقل میباشد. معادلهای پدید آمده از تابعی با بیش از یک متغیّر مستقل همراه با مشتقات جزئی آن را معادله دیفرانسیل جزئی (به انگلیسی: PDE) مینامند.
خطی
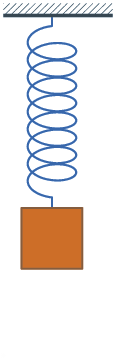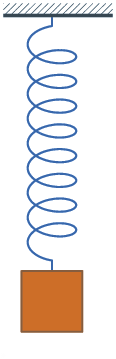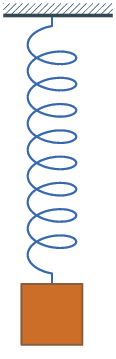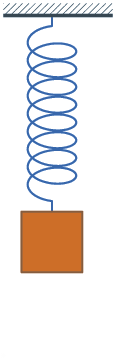

برای مدلسازی نوسان هارمونیک سادهٔ یک فنر از قانون دوم نیوتن و قانون هوک استفاده و به یک معادلهٔ دیفرانسیل خطی همگن مرتبه دوم (خودگردان) میرسیم: {\displaystyle F=ma=m{\operatorname {d} ^{2}\!x \over \operatorname {d} \!t^{2}}=-kx}
هر دو نوع این معادلات را میتوان از دیدگاه خطی یا غیرخطی بودن تابع پاسخ هم دستهبندی کرد. اکثر معادلاتی (معمولی) که در فیزیک به آنها برمیخوریم خطی هستند.
اگر درجهٔ مجهول و مشتقاتش یک باشند، آن را خطی و در غیر این صورت غیرخطی مینامیم.
به عنوان مثال، معادلهٔ {\displaystyle y’=1} خطی است ولی معادلهٔ {\displaystyle (y’)^{2}=1} غیرخطی است.
به دلیل این که معادلات خطی حل (نسبتاً) سادهتری دارند، میتوان معادلات غیرخطی را با تقریب خطی به معادلات خطی تبدیل و آنها را با روشهای معمول حل کرد. به این عمل خطیسازی میگویند.
از کاربردهای فیزیکی این معادلات میتوان به مدلسازی حرکت سیارات، که از قانون دوم نیوتن به دست میآیند اشاره کرد. در مورد حرکت موشکها در نزدیکی سطح زمین و در فضا، معادلات دیفرانسیل پیچیدهتر هستند. در رشته سینتیک شیمیایی، معادلات دیفرانسیل نقش منحصر به فردی به عهده دارند. همچنین در مواردی چون سود مرکب، واپاشی رادیواکتیو و قانون سرمایش نیوتن کاربرد فراوانی دارد.
مطلب پیشنهادی عالی برای شما :
دانلود Pdf کتاب معادلات دیفرانسیل | حسین فرامرزی
دانلود و خرید PDF کتاب ریاضی عمومی ۱ | حسین فرامرزی
مرتبه
مرتبهٔ یک معادلهٔ دیفرانسیل عبارت است از مرتبهٔ مشتقی که بالاترین مرتبه را در معادله دارد.
به عنوان مثال، مرتبهٔ معادلهٔ {\displaystyle y’=1} یک است و مرتبهٔ {\displaystyle y”=1} دو است.
همچنین مرتبه معادلات دیفرانسیل را میتوان به صورت کسری در نظر گرفت که به معادلات دیفرانسیل کسری مشهورند. این نوع از معادلات دیفرانسیل غیرخطی نیز روشهای حل گوناگونی دارند که میتوان به روش تجزیه آدومیان، هموتوپی و تکرار تغییرات اشاره نمود.
دستگاه معادلات دیفرانسیل
یک شاخهبندی دیگر این معادلات، تعداد مجهولهای این معادلات است. اگر یک مجهول وجود داشته باشد، یک معادله برای پیدا کردن جواب کافی است. اگر دو مجهول باشد دو معادله نیاز است که تشکیل دستگاه معادلات دیفرانسیل میدهند.
از این معادلات میتوان به معادله لوتکا-ولترا اشاره کرد که در مدلسازی جمعیّت شکار و شکارچی استفاده میشود.
مرتبه اول
معادلات دیفرانسیل مرتبهٔ اوّل (به انگلیسی: First-Order Differential Equations) گروهی از معادلات دیفرانسیل هستند که تنها شامل مشتق مرتبهٔ اوّل تابع مجهول هستند (و البتّه خود آن تابع). اگر {\displaystyle y(x)} تابعی مجهول از متغیّر {\displaystyle x} باشد، یک معادله دیفرانسیل مرتبه اوّل معادلهای ست که بتوان آن را به صورت زیر نمایش داد (که در آن {\displaystyle f} میتواند هر تابع پیوستهای باشد):
{\displaystyle {\operatorname {d} \!y \over \operatorname {d} \!x}=y\prime =f(x,y)}
به عنوان مثال {\displaystyle y\prime =2x} یک معادله دیفرانسیل مرتبه اوّل است ({\displaystyle f=2x}) و حل آن ما را به {\displaystyle y=x^{2}+c} میرساند.
یکی از فرمهای دیگر این معادلات به شکل زیر است:
{\displaystyle M(x,y)\operatorname {d} \!x+N(x,y)\operatorname {d} \!y=0}
برای حل این معادلات روش کلی وجود ندارد. روشهای متعدّدی وجود دارد که هر کدام تنها برای دستهٔ خاصی از این معادلات کاربردی هستند. از مهمترین آنها میتوان به مرتبه اول خطی و مرتبه اول تفکیکپذیر اشاره کرد که در ادامه به آنها میپردازیم.
قضیه وجود و یکتایی
قضیهٔ پیکارد-لیندلوف (به انگلیسی: Picard–Lindelöf theorem): این معادلات در بازهٔ وجودیشان دقیقاً یک جواب دارند. اگر {\displaystyle f} پیوسته باشد، بازهٔ وجودی برابر {\displaystyle \mathbb {R} } است.
در غیر این صورت، پیدا کردن بازهای که جواب در آن وجود دارد میتواند سخت باشد. بازهٔ وجودی جواب شاید هیچ ارتباطی با بازهٔ پیوستگی {\displaystyle f} نداشته باشد.
اگر توابع {\displaystyle f} و {\displaystyle {\partial f \over \partial y}} در یک مربّع فرضی (مثل {\displaystyle x\in [X_{1},X_{2}],\ \ \ y\in [Y_{1},Y_{2}]}) پیوسته باشند،
بازهای از {\displaystyle x} (مثل {\displaystyle x\in [\alpha ,\beta ]\subseteq [X_{1},X_{2}]}) وجود دارد که معادلهٔ {\displaystyle y\prime =f(x,y)} (با مقادیر اوّلیّهٔ دلخواه) در آن جواب دارد.
توجّه کنید که شروط ذکر شده ضروری نیستند؛ یعنی شاید بتوان به روشی دیگر و بدون کمک گرفتن از این قضیه، بازهٔ وجودی پیدا کرد.
مرتبه اول خطی
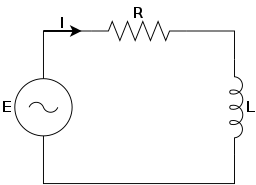

یک مدار RL ساده
در صورتی که درجهٔ {\displaystyle y} و {\displaystyle y\prime } یک باشد به آن خطی گوییم.
در مدارهای RL، به کمک قانون اهم به معادلاتی مشابه {\displaystyle L{\operatorname {d} \!i \over \operatorname {d} \!t}+Ri=V} میرسیم ({\displaystyle L} و {\displaystyle R} و {\displaystyle V} ثابت و {\displaystyle i} تابعی از {\displaystyle t}) و برای پیدا کردن {\displaystyle i} باید از معادلات دیفرانسیل مرتبه اوّل خطی کمک بگیریم.
مطلب پیشنهادی عالی برای شما :
دانلود Pdf کتاب معادلات دیفرانسیل | حسین فرامرزی
دانلود و خرید PDF کتاب ریاضی عمومی ۱ | حسین فرامرزی
برنولی
معادلهٔ دیفرانسیل برنولی (به انگلیسی: Bernoulli differential equation) معادلهای ست که بتوان آن را به صورت {\displaystyle y’+p(t)y=q(t)y^{n}} نوشت.
برای حل این معادلات میتوان آنها را با تغییر متغیّر {\displaystyle u=y^{n-1}} به معادلهٔ خطی تبدیل کرد:[۲]
{\displaystyle y’+p(t)y=q(t)y^{n}\Longrightarrow y^{-n}y’+p(t)y^{1-n}=q(t)\Longrightarrow {1 \over 1-n}{\operatorname {d} \!u \over \operatorname {d} \!t}+p(t)u=q(t)\Longrightarrow {\operatorname {d} \!u \over \operatorname {d} \!t}+(1-n)p(t)u=(1-n)q(t)}
مرتبه اول تفکیکپذیر
معادلهٔ دیفرانسیل مرتبهٔ اوّل تفکیکپذیر (به انگلیسی: separable first-order differential equations) معادلاتی هستند که بتوان آنها را به فرم دیفرانسیلی زیر نمایش داد ({\displaystyle M} و {\displaystyle N} دلخواه):
{\displaystyle M(x)\operatorname {d} \!x=N(y)\operatorname {d} \!y}
برای حل این معادله، آن را به فرم زیر مینویسیم:
{\displaystyle f(x)=g(y){\operatorname {d} \!y \over \operatorname {d} \!x}}
با فرض این که {\displaystyle F} و {\displaystyle G} پادمشتق {\displaystyle f} و {\displaystyle g} باشند:
{\displaystyle F'(x)=G'(y){\operatorname {d} \!y \over \operatorname {d} \!x}}
طبق قاعدهٔ زنجیرهای:
{\displaystyle G'(y){\operatorname {d} \!y \over \operatorname {d} \!x}={\operatorname {d} \over \operatorname {d} \!y}G(y){\operatorname {d} \!y \over \operatorname {d} \!x}={\operatorname {d} \over \operatorname {d} \!x}G(y)}
در نتیجه تساوی بالا را میتوان به صورت زیر نوشت:
{\displaystyle {\operatorname {d} \over \operatorname {d} \!x}F(x)={\operatorname {d} \over \operatorname {d} \!x}G(y)}
در نتیجه، با انتگرالگیری نسبت به {\displaystyle x} داریم:
{\displaystyle F(x)=G(y)+c}
به عبارتی دیگر، جواب به صورت زیر به دست میآید:
{\displaystyle \int f(s)\operatorname {d} \!s=\int g(s)\operatorname {d} \!s}
مرتبه اول همگن
اگر یک معادلهٔ دیفرانسیل مرتبه اوّل را به فرم {\displaystyle M(x,y)\operatorname {d} \!x+N(x,y)\operatorname {d} \!y=0} بنویسیم، در صورتی که توابع {\displaystyle M(x,y)} و {\displaystyle N(x,y)} هر دو توابع همگن با درجه (مرتبه) یکسان باشند، آن معادله دیفرانسیل مرتبه اول همگن (به انگلیسی: Homogeneous first-order differential equation) است.
به عبارتی دیگر {\displaystyle M(\lambda x,\lambda y)=\lambda ^{n}M(x,y)} و {\displaystyle N(\lambda x,\lambda y)=\lambda ^{n}N(x,y)}.
توجّه کنید که مرتبهٔ همگنی توابع ({\displaystyle n}) با مرتبهٔ معادله (یک) اشتباه نشود.
حال درصورتی که {\displaystyle \lambda ={1 \over x}}:
{\displaystyle y\prime =f(x,y)={M(x,y) \over N(x,y)}={x^{n}({1 \over x^{n}}M(x,y)) \over x^{n}({1 \over x^{n}}N(x,y))}={x^{n}(\lambda ^{n}M(x,y)) \over x^{n}(\lambda ^{n}N(x,y))}={x^{n}M(\lambda x,\lambda y) \over x^{n}N(\lambda x,\lambda y)}={M(1,{y \over x}) \over N(1,{y \over x})}=f(1,{y \over x})}
به عبارتی دیگر {\displaystyle y\prime } را میتوان به صورت تابعی از تنها کسر {\displaystyle y \over x} بیان کرد ({\displaystyle f} یک تابع همگن درجه صفر است). این معادلات را میتوان با تغییر متغیّر {\displaystyle v={y \over x}} به معادلات تفکیکپذیر تبدیل کرد.[۲]
به عنوان مثال، معادلهٔ {\displaystyle {\operatorname {d} \!y \over \operatorname {d} \!x}={y-4x \over x-y}} را میتوان به صورت {\displaystyle {\operatorname {d} \!y \over \operatorname {d} \!x}={{y \over x}-4 \over 1-{y \over x}}} نمایش داد (پس همگن است). با فرض {\displaystyle v={y \over x}}، میتوان معادله را به صورت {\displaystyle {1 \over x}\operatorname {d} \!x={1-v \over v^{2}-4}\operatorname {d} \!v} تفکیک کرد. ادامهٔ حل، به روش حل معادلات تفکیکپذیر است.
مطلب پیشنهادی عالی برای شما :
دانلود Pdf کتاب معادلات دیفرانسیل | حسین فرامرزی
دانلود و خرید PDF کتاب ریاضی عمومی ۱ | حسین فرامرزی
یک حالت خاص
اگر یک معادلهٔ دیفرانسیل به فرم {\displaystyle (ax+by+c)\operatorname {d} \!x+(ex+fy+g)\operatorname {d} \!y=0} یا {\displaystyle y’={\operatorname {d} \!y \over \operatorname {d} \!x}=-{ax+by+c \over ex+fy+g}} باشد، میتوان معادلهٔ مذکور را با تغییر متغیّر به یک معادلهٔ همگن تبدیل کرد.
جوابهای دو معادله دومجهولی {\displaystyle ax+by+c=0} و {\displaystyle ex+fy+g=0} به صورت زیر به دست میآید (اگر {\displaystyle af\neq be}):
{\displaystyle \alpha ={cf-bg \over be-af},\quad \beta ={ag-ce \over be-af}}
سپس با تغییر متغیّر {\displaystyle X=x-\alpha } و {\displaystyle Y=y-\beta } میتوان معادلهٔ مذکور را به یک معادلهٔ همگن تبدیل کرد:
{\displaystyle {\operatorname {d} \!y \over \operatorname {d} \!x}={\operatorname {d} \!Y \over \operatorname {d} \!X}=-{aX+bY \over eX+fY}}
مرتبه اول خودگردان
در صورتی که نرخ رشد یک تابع ({\displaystyle y(x)}) تنها به مقدار تابع وابسته باشد، خودگردان (به انگلیسی: autonomous differential equations) نامیده میشود: {\displaystyle y\prime =f(y)}
رشد نمایی


معادلهٔ رشد نمایی سادهترین نوع معادلات خودگردان است و برای مدلسازی رشد بعضی گونهها (مثل میکروبها) استفاده میشود. به این معادله «قانون رشد طبیعی» نیز میگویند.
این معادلات را میتوان به فرم {\displaystyle y\prime =ry} نوشت ({\displaystyle r} یک عدد و {\displaystyle y} تابعی از {\displaystyle t} است) و جواب آن برابر {\displaystyle y=y_{0}e^{rt}} است.
رشد لجستیک
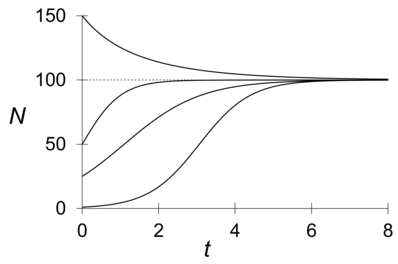

چند تابع لجستیک مختلف با ثابت {\displaystyle K=100}
معادلهٔ لُجِستیک یا معادلهٔ ورهولست (به انگلیسی: Verhulst equation or Logistic equation) از انواع معادلات خودگردان است که اوّلین بار توسّط یک ریاضیدان بلژیکی (به فرانسوی: Pierre François Verhulst) برای مدلسازی رشد جمعیّت معرّفی شد.
به عنوان مثال در حالت کشت سلّول در یک پتریدیش، اگر در ابتدا تعداد میکروبها کم باشند به صورت نمایی رشد میکنند؛ امّا به دلیل محدود بودن فضای رشد، تعداد آنها از مقدار خاصی فراتر نمیرود و سرعت رشد به مرور کاهش پیدا میکند. همچنین اگر تعداد اوّلیّهٔ میکروبها از این حد فراتر بود تعدادی از آنها نابود میشدند.
این معادلات را میتوان به فرم {\displaystyle y\prime =(r-ay)\ y} یا به شکل معمولترِ {\displaystyle y\prime =r(1-{y \over K})\ y} نوشت ({\displaystyle K={r \over a}}).
به ثابت {\displaystyle r>0} نرخ رشد ذاتی (به انگلیسی: intrinsic growth rate) گفته میشود، زیرا در ابتدا (یعنی {\displaystyle t=0}) که {\displaystyle y\thickapprox 0} است، {\displaystyle y\prime \thickapprox ry} میشود.
به ثابت {\displaystyle K} حد اشباع یا ظرفیّت تحمّل محیطی (به انگلیسی: environmental carrying capacity) گفته میشود. تمام توابع لجستیک (با هر مقدار اوّلیّهٔ مثبتی) به {\displaystyle K} میل میکنند.
حل این معادلات به صورت زیر است:[۲]{\displaystyle y\prime ={\operatorname {d} \!y \over \operatorname {d} \!t}=r(1-{y \over K})\ y\Longrightarrow r\operatorname {d} \!t={\operatorname {d} \!y \over {(1-{y \over K})\ y}}=({1 \over y}+{{1 \over K} \over 1-{y \over K}})\operatorname {d} \!y\Longrightarrow \int r\operatorname {d} \!t=\int {1 \over y}+{{1 \over K} \over 1-{y \over K}}\operatorname {d} \!y\Longrightarrow rt+c=\ln y-\ln(1-{y \over K})\Longrightarrow e^{rt+c}={y \over 1-{y \over K}}}{\displaystyle \Longrightarrow y={y_{0}K \over y_{0}+(K-y_{0})e^{-rt}}}
مطلب پیشنهادی عالی برای شما :
دانلود Pdf کتاب معادلات دیفرانسیل | حسین فرامرزی
دانلود و خرید PDF کتاب ریاضی عمومی ۱ | حسین فرامرزی
مرتبه اول کامل
اگر یک معادلهٔ دیفرانسیل مرتبه اوّل را به فرم {\displaystyle M(x,y)\operatorname {d} \!x+N(x,y)\operatorname {d} \!y=0} بنویسیم، با فرض این که {\displaystyle M_{y}(x,y)={\partial {M} \over \partial y}} و {\displaystyle N_{x}(x,y)={\partial N \over \partial x}} مشتقهای جزئی این توابع باشند (که در یک ناحیهٔ خاص پیوسته است)،
معادلهٔ مورد نظر کامل (به انگلیسی: exact differential equations) است اگر و تنها اگر {\displaystyle M_{y}(x,y)=N_{x}(x,y)}.
به بیانی دیگر معادله کامل است اگر و تنها اگر تابعی مانند {\displaystyle \psi (x,y)} وجود داشته باشد که {\displaystyle \psi _{x}=M} و {\displaystyle \psi _{y}=N}. در آن صورت {\displaystyle \psi _{xy}=M_{y}=N_{x}=\psi _{yx}} میشود.
برای حل این معادلات میتوان از این روش استفاده کرد:
{\displaystyle M(x,y)+N(x,y){\operatorname {d} \!y \over \operatorname {d} \!x}=0={\operatorname {d} \!\psi \over \operatorname {d} \!x}+{\operatorname {d} \!\psi \over \operatorname {d} \!y}{\operatorname {d} \!y \over \operatorname {d} \!x}=2{\operatorname {d} \!\psi \over \operatorname {d} \!x}\Longrightarrow {\operatorname {d} \!\psi \over \operatorname {d} \!x}=0\Longrightarrow \psi =c}
در نتیجه با قرار دادن {\displaystyle \psi (x,y)=c} به جواب میرسیم.
عامل انتگرالساز
در بعضی موارد که معادلهٔ {\displaystyle M(x,y)\operatorname {d} \!x+N(x,y)\operatorname {d} \!y=0} کامل نیست میتوان با یک ترفند آن را به یک معادلهٔ کامل تبدیل کرد و سپس آن را به روش مذکور حل کرد. در این ترفند ساده معادله را در یک عامل انتگرالساز (به انگلیسی: integrating factor) (مثل {\displaystyle \mu }) ضرب میکنیم به صورتی که معادلهٔ به دست آمده ({\displaystyle \mu (x,y)M(x,y)\operatorname {d} \!x+\mu (x,y)N(x,y)\operatorname {d} \!y=0}) کامل باشد.
مشکل این ترفند در پیدا کردن عامل انتگرالساز مناسب است. طبق تعریفِ معادلهٔ کامل برای معادلهٔ جدید:
{\displaystyle (\mu M)_{y}=(\mu N)_{x}\Longrightarrow M\mu _{y}-N\mu _{x}+(M_{y}-N_{x})\mu =0}
امّا پیدا کردن {\displaystyle \mu } با حل این معادله بسیار دشوار است (همچنین احتمالاً {\displaystyle \mu } یکتا نیست). برای حل این مشکل حدس میزنیم که {\displaystyle \mu _{y}=0} باشد و امیدوار میمانیم که همینطور باشد. اگر با این فرض {\displaystyle \mu } به دست آمد و معادلهٔ {\displaystyle \mu M\operatorname {d} \!x+\mu N\operatorname {d} \!y=0} طبق تعریف کامل شد، به این نتیجه میرسیم که فرضمان درست بوده. گاهی نیز با حدس {\displaystyle \mu _{x}=0} میتوان به جواب رسید.
یک مثال
معادلهٔ {\displaystyle 3xy+y^{2}+(x^{2}+xy)y’=0} کامل نیست. {\displaystyle M(x,y)=3xy+y^{2}} و {\displaystyle N(x,y)=x^{2}+xy}.
برای پیدا کردن عامل انتگرالساز از حدس {\displaystyle \mu _{y}=0} استفاده میکنیم:
{\displaystyle (\mu M)_{y}=(\mu N)_{x}\Longrightarrow -N\mu _{x}+(M_{y}-N_{x})\mu =0\Longrightarrow {\mu _{x} \over \mu }={M_{y}-N_{x} \over N}={1 \over x}\Longrightarrow \mu =x}
معادلهٔ جدید به صورت {\displaystyle 3x^{2}y+xy^{2}+(x^{3}+x^{2}y)y’=0} به دست میآید.
باید بررسی کنیم که آیا معادلهٔ جدید کامل هست یا نه، زیرا شاید حدسمان اشتباه بوده. پس از بررسی (تعریف کامل بودن) مشاهده میکنیم که معادله کامل شده. حال باید معادلهٔ کامل را حل کنیم تا جواب به دست بیاید.
تابعی مانند {\displaystyle \psi (x,y)} وجود دارد که {\displaystyle \psi _{x}=M=3x^{2}y+xy^{2}} و {\displaystyle \psi _{y}=N=x^{3}+x^{2}y}.
{\displaystyle \psi =\int \psi _{x}\operatorname {d} \!x=\int M\operatorname {d} \!x=x^{3}y+{1 \over 2}x^{2}y^{2}+h(y)\Longrightarrow \psi _{y}=x^{3}+x^{2}y+h'(y)}
از طرفی میدانستیم که {\displaystyle \psi _{y}=N=x^{3}+x^{2}y}. پس:
{\displaystyle \psi _{y}=x^{3}+x^{2}y+h'(y)=x^{3}+x^{2}y\Longrightarrow h’=0\Longrightarrow h=c}
{\displaystyle \Longrightarrow \psi =x^{3}y+{1 \over 2}x^{2}y^{2}+c}
برای حل معادلات کامل باید از {\displaystyle \psi =c} استفاده کرد:
{\displaystyle x^{3}y+{1 \over 2}x^{2}y^{2}=c}
در ادامه میتوان {\displaystyle y} را بر حسب {\displaystyle x} به دست آورد.
همچنین توجّه داشته باشید که {\displaystyle \mu } یکتا نبود. به عنوان مثال {\displaystyle \mu ={1 \over xy(2x+y)}} یک عامل انتگرالساز دیگر است که به کمک آن باز هم به همین جواب میرسیم.
مطلب پیشنهادی عالی برای شما :
دانلود Pdf کتاب معادلات دیفرانسیل | حسین فرامرزی
دانلود و خرید PDF کتاب ریاضی عمومی ۱ | حسین فرامرزی
معادلات دیفرانسیل مشهور (انواع معادله دیفرانسیل) :
- قانون دوم نیوتن در دینامیک (مکانیک)
- معادلات همیلتون در مکانیک کلاسیک
- واپاشی هستهای در فیزیک هستهای
- معادله موج
- معادلات ماکسول در الکترومغناطیس
- معادلات پواسن
- معادله لاپلاس که توابع هارمونیک را تعریف میکند
- مسئله منحنی کوتاهترین زمان.
- فرمول انیشتین.
- قانون گرانش نیوتن.
- معادله شرودینگر در مکانیک کوانتوم
- معادلات ناویه-استوکس در دینامیک شارهها
- معادلات کوشی-ریمان در آنالیز مختلط
- معادله پواسون-بولتزمن در دینامیک ملکولی
- معادله موج برای تار مرتعش.
- نوسانگر همساز در مکانیک کوانتومی.
- نظریه پتانسیل.
- معادله موج برای غشای مرتعش.
- معادلات شکار و شکارچی.
- مکانیک غیر خطی.
- مسئلهٔ مکانیکی آبل.
- معادلات دسته لین-امدن
- معادله ابرگاز کروی
- معادله کوتوله سفید
- معادلات امدن-فاولر
- معادله جمعیتی ولترا
- معادله توماس فرمی
- معادله بلاسیوس
- معادله فالکنر اسکن
- معادله فوکر-پلانک
- معادله لوتکا ولترا در مدلسازی جمعیّت شکار و شکارچی
- معادله زابولوتسکایا-خوخولوف
- معادله برنولی
مطلب پیشنهادی عالی برای شما :
دانلود Pdf کتاب معادلات دیفرانسیل | حسین فرامرزی
دانلود و خرید PDF کتاب ریاضی عمومی ۱ | حسین فرامرزی





































![{\displaystyle x\in [X_{1},X_{2}],\ \ \ y\in [Y_{1},Y_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12db1ba7017ebeaaa2827af54eae1c10bb180e52)
![{\displaystyle x\in [\alpha ,\beta ]\subseteq [X_{1},X_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a164d37b3d88897340398efdd235715f6d7b2019)



































































































